跳到主要内容

GGUF

Hugging Face Hub 支持所有文件格式，但对 GGUF 格式 具有内置功能，这是一种针对快速加载和保存模型进行优化的二进制格式，使其在推理方面非常高效。GGUF 设计用于与 GGML 和其他执行器一起使用。GGUF 由 @ggerganov 开发，他也是流行的 C/C++ LLM 推理框架 llama.cpp 的开发者。最初在 PyTorch 等框架中开发的模型可以转换为 GGUF 格式以与这些引擎一起使用。

正如我们在此图中看到的，与仅包含张量的文件格式（如 safetensors——这也是 Hub 推荐的模型格式）不同，GGUF 同时编码张量和标准化的元数据集。

查找 GGUF 文件​

你可以通过 GGUF 标签筛选浏览所有带有 GGUF 文件的模型：hf.co/models?library=gguf。此外，你可以使用 ggml-org/gguf-my-repo 工具将模型权重转换/量化为 GGUF 权重。

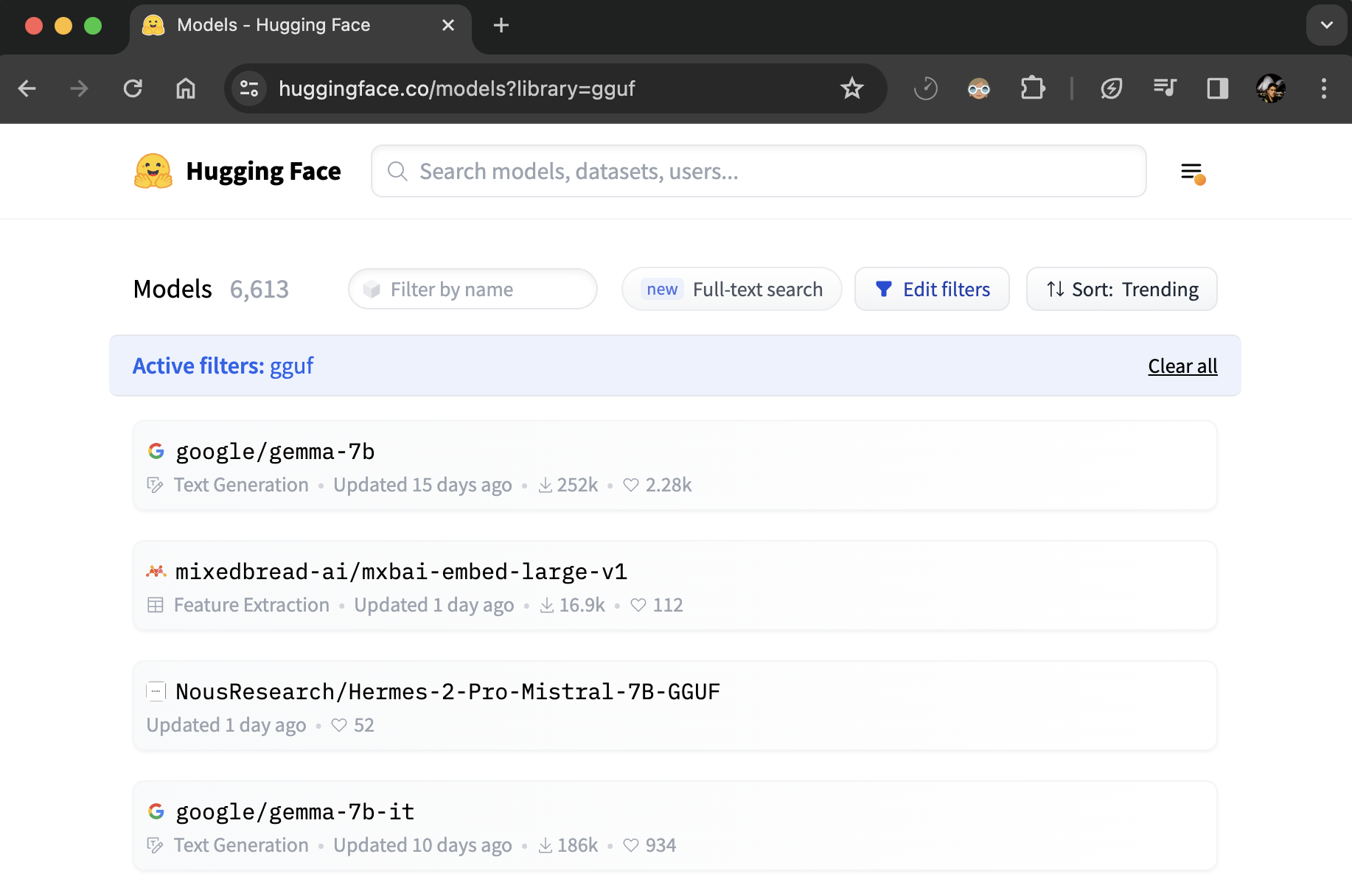
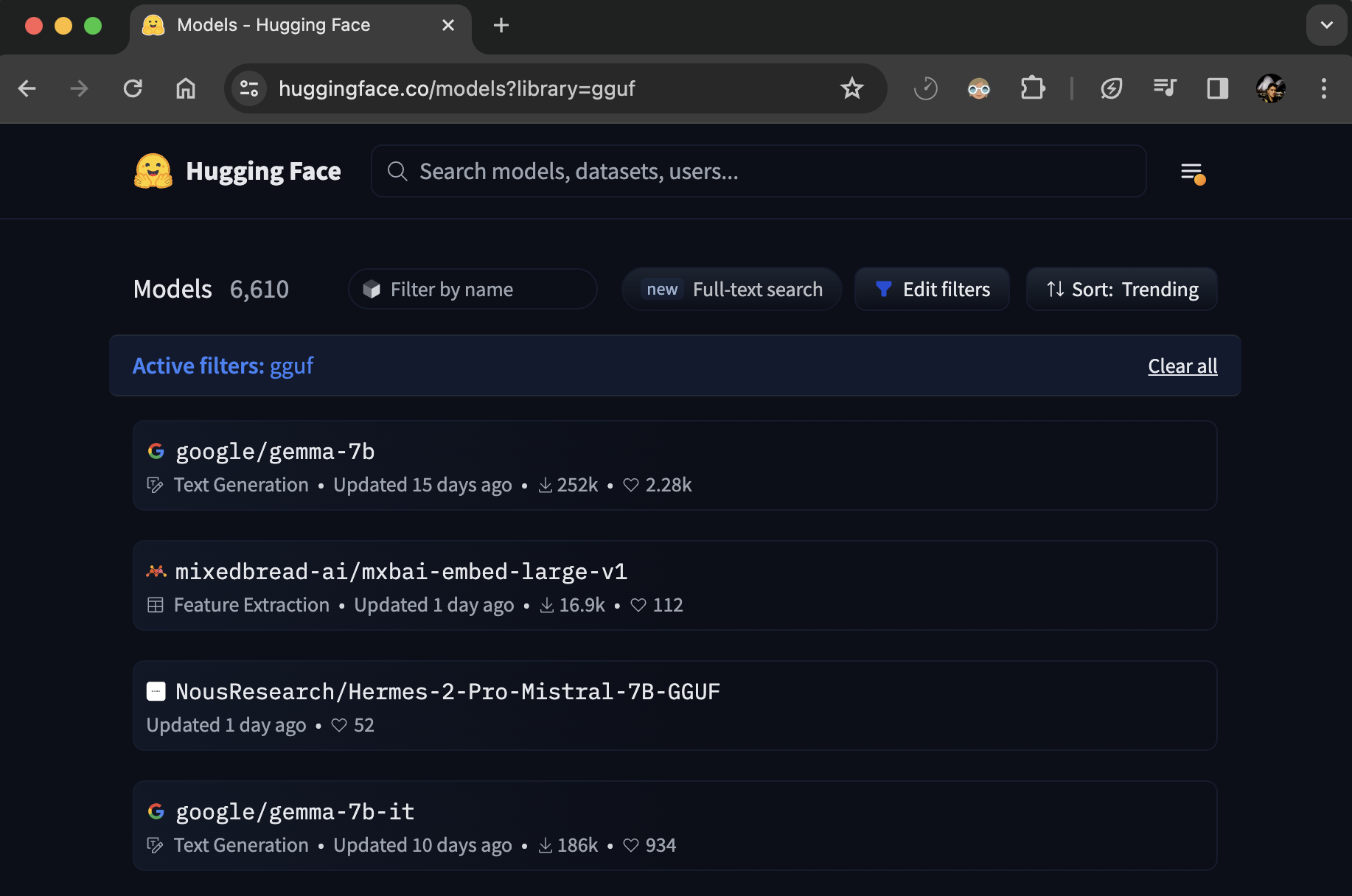
在 GGUF 中使用模型在 GGUF 中使用模型

例如，你可以查看 TheBloke/Mixtral-8x7B-Instruct-v0.1-GGUF 以查看 GGUF 文件的实际使用情况。

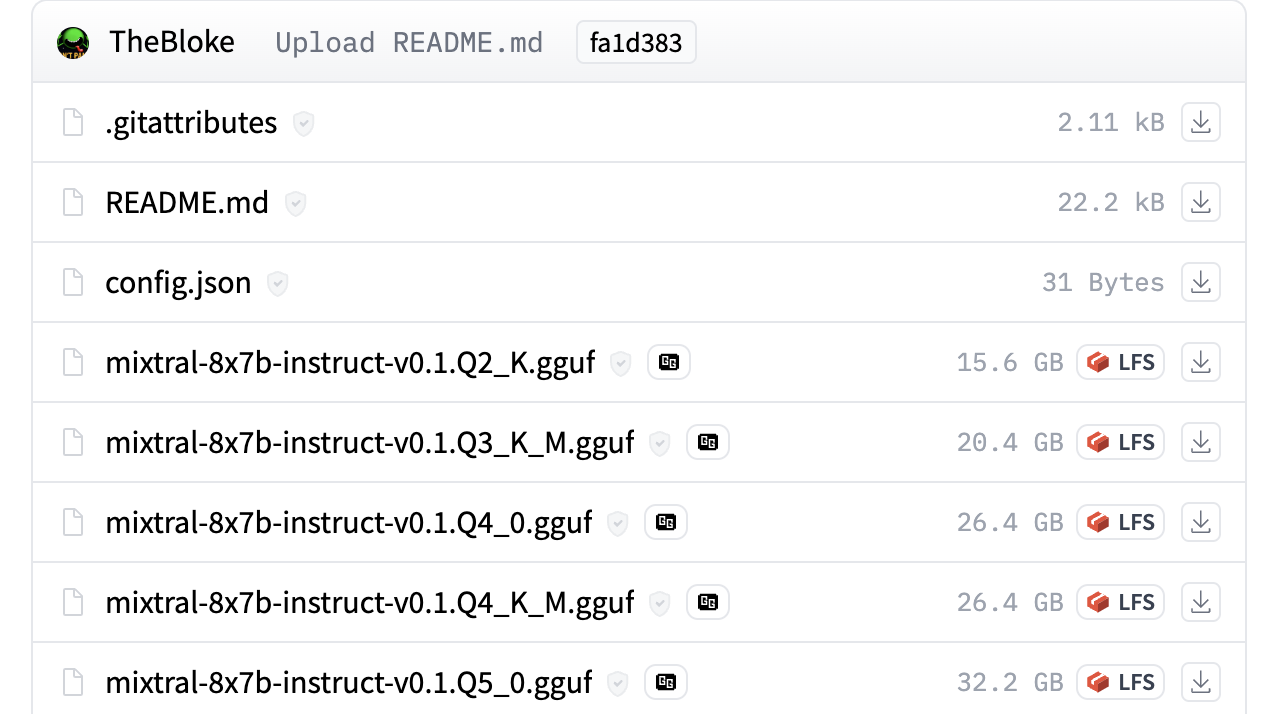
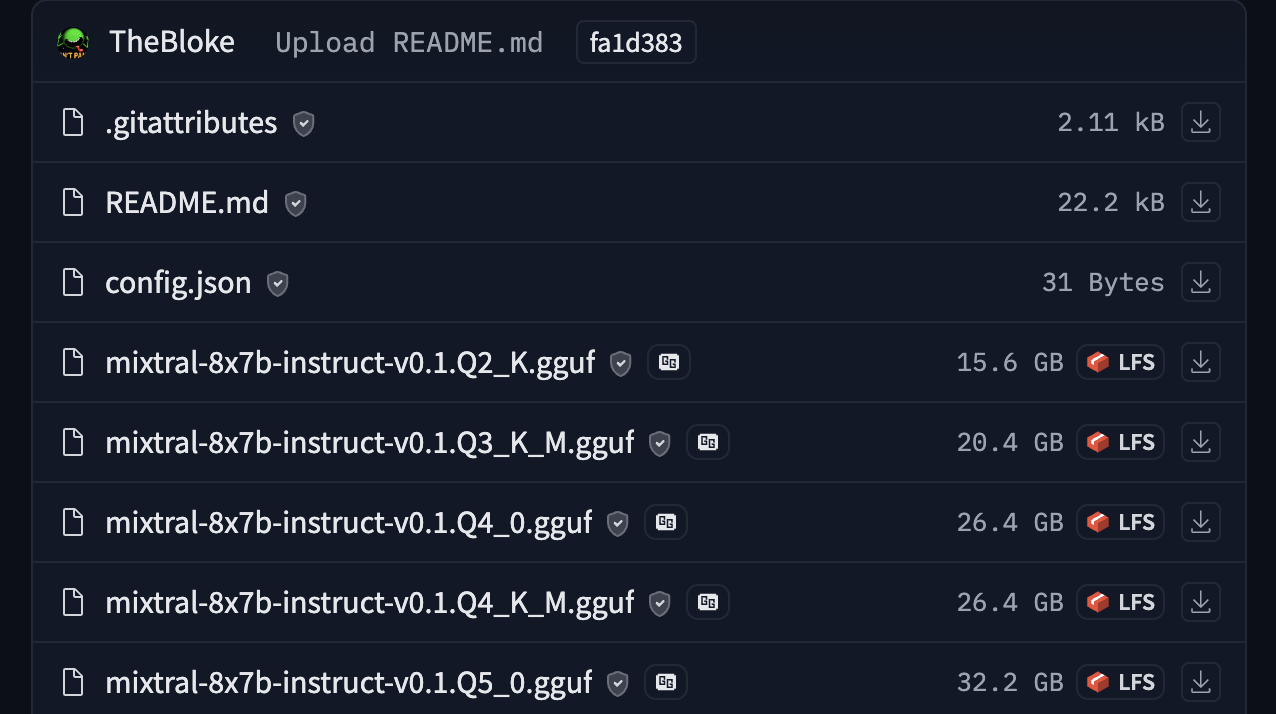
在 GGUF 中使用模型在 GGUF 中使用模型

元数据和张量信息查看器​

Hub 有一个 GGUF 文件查看器，允许用户查看元数据和张量信息（名称、形状、精度）。查看器在模型页面（示例）和文件页面（示例）上可用。

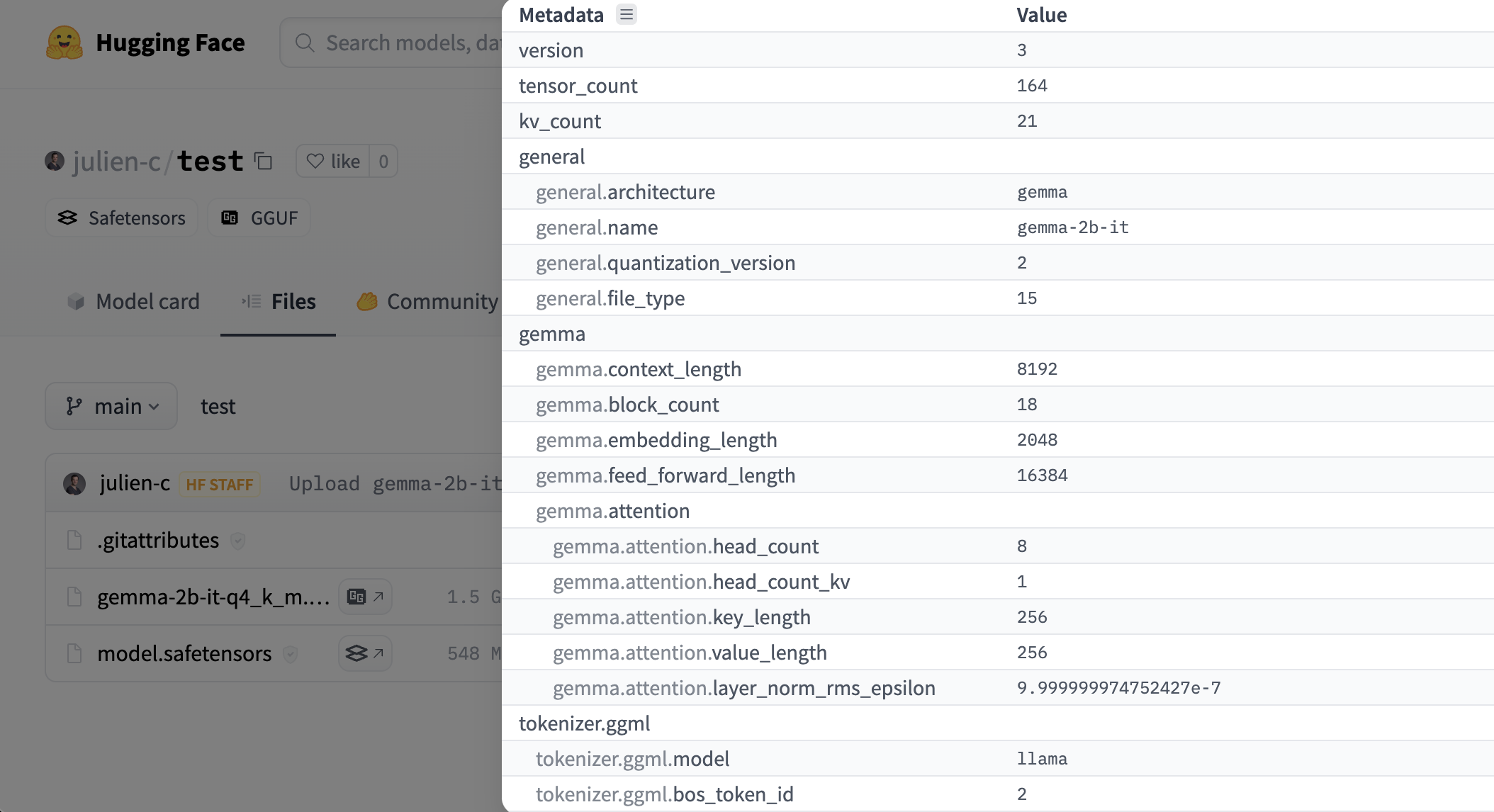
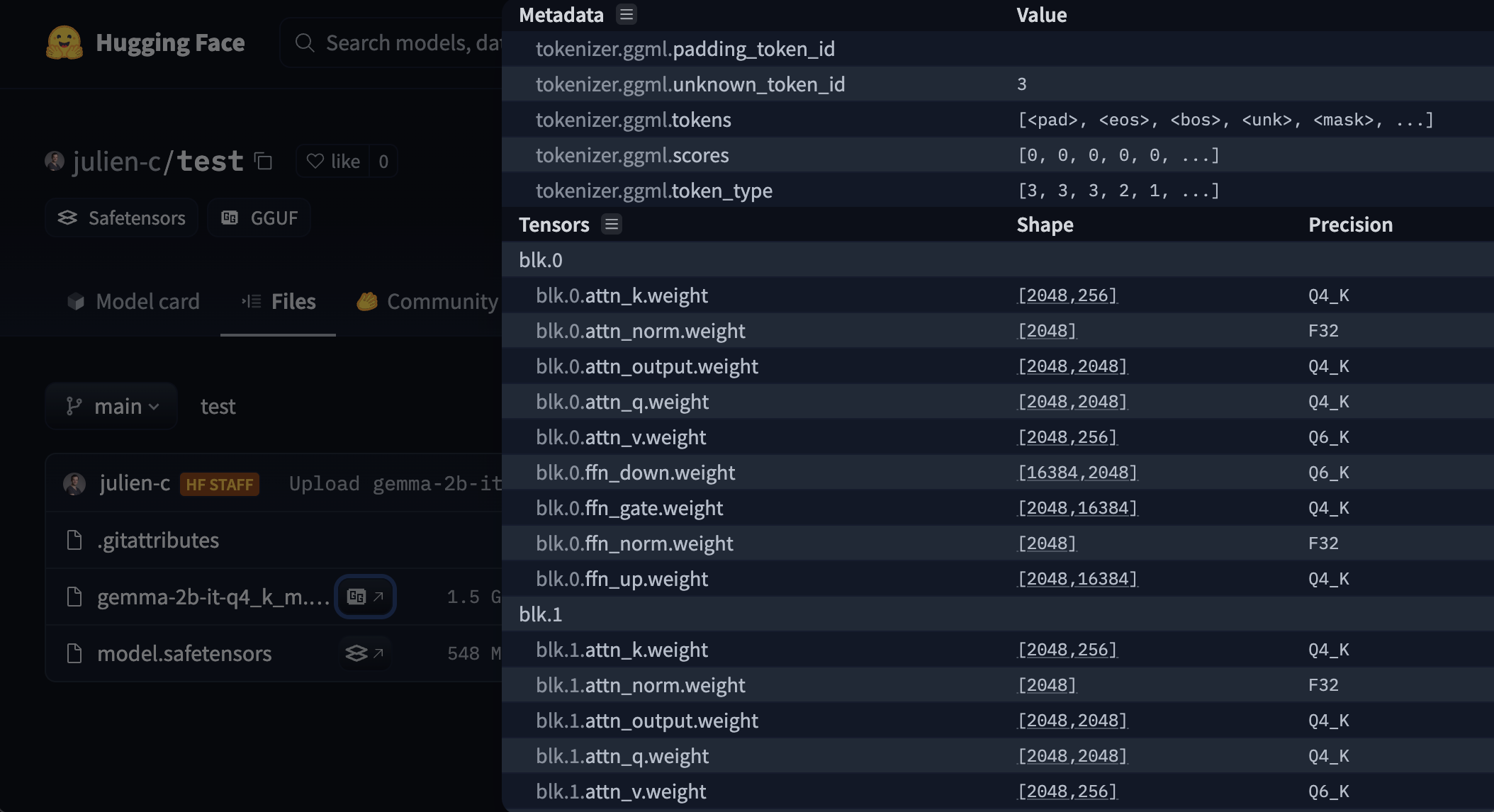
在 GGUF 中使用模型在 GGUF 中使用模型

与开源工具的使用​

使用 @huggingface/gguf 解析元数据​

我们还创建了一个 JavaScript GGUF 解析器，可在远程托管文件（例如 Hugging Face Hub）上工作。

npm install @huggingface/gguf
import { gguf } from "@huggingface/gguf";
// 来自 https://huggingface.co/TheBloke/Llama-2-7B-Chat-GGUF 的远程 GGUF 文件
const URL_LLAMA = "https://huggingface.co/TheBloke/Llama-2-7B-Chat-GGUF/resolve/191239b/llama-2-7b-chat.Q2_K.gguf";
const { metadata, tensorInfos } = await gguf(URL_LLAMA);

更多信息请访问这里。

量化类型​

类型来源描述
F64Wikipedia64 位标准 IEEE 754 双精度浮点数。
I64GH64 位固定宽度整数。
F32Wikipedia32 位标准 IEEE 754 单精度浮点数。
I32GH32 位固定宽度整数。
F16Wikipedia16 位标准 IEEE 754 半精度浮点数。
BF16Wikipedia32 位 IEEE 754 单精度浮点数的 16 位缩短版本。
I16GH16 位固定宽度整数。
Q8_0GH8 位四舍五入量化（q）。每个块有 32 个权重。权重公式：w = q * block_scale。传统量化方法（目前未广泛使用）。
Q8_1GH8 位四舍五入量化（q）。每个块有 32 个权重。权重公式：w = q * block_scale + block_minimum。传统量化方法（目前未广泛使用）
Q8_KGH8 位量化（q）。每个块有 256 个权重。仅用于量化中间结果。所有 2-6 位点积都为此量化类型实现。权重公式：w = q * block_scale。
I8GH8 位固定宽度整数。
Q6_KGH6 位量化（q）。超级块有 16 个块，每个块有 16 个权重。权重公式：w = q * block_scale(8-bit)，结果为每权重 6.5625 位。
Q5_0GH5 位四舍五入量化（q）。每个块有 32 个权重。权重公式：w = q * block_scale。传统量化方法（目前未广泛使用）。
Q5_1GH5 位四舍五入量化（q）。每个块有 32 个权重。权重公式：w = q * block_scale + block_minimum。传统量化方法（目前未广泛使用）。
Q5_KGH5 位量化（q）。超级块有 8 个块，每个块有 32 个权重。权重公式：w = q * block_scale(6-bit) + block_min(6-bit)，结果为每权重 5.5 位。
Q4_0GH4 位四舍五入量化（q）。每个块有 32 个权重。权重公式：w = q * block_scale。传统量化方法（目前未广泛使用）。
Q4_1GH4 位四舍五入量化（q）。每个块有 32 个权重。权重公式：w = q * block_scale + block_minimum。传统量化方法（目前未广泛使用）。
Q4_KGH4 位量化（q）。超级块有 8 个块，每个块有 32 个权重。权重公式：w = q * block_scale(6-bit) + block_min(6-bit)，结果为每权重 4.5 位。
Q3_KGH3 位量化（q）。超级块有 16 个块，每个块有 16 个权重。权重公式：w = q * block_scale(6-bit)，结果为每权重 3.4375 位。
Q2_KGH2 位量化（q）。超级块有 16 个块，每个块有 16 个权重。权重公式：w = q * block_scale(4-bit) + block_min(4-bit)，结果为每权重 2.625 位。
IQ4_NLGH4 位量化（q）。超级块有 256 个权重。权重 w 使用 super_block_scale 和 importance matrix 获得。
IQ4_XSHF4 位量化（q）。超级块有 256 个权重。权重 w 使用 super_block_scale 和 importance matrix 获得，结果为每权重 4.25 位。
IQ3_SHF3 位量化（q）。超级块有 256 个权重。权重 w 使用 super_block_scale 和 importance matrix 获得，结果为每权重 3.44 位。
IQ3_XXSHF3 位量化（q）。超级块有 256 个权重。权重 w 使用 super_block_scale 和 importance matrix 获得，结果为每权重 3.06 位。
IQ2_XXSHF2 位量化（q）。超级块有 256 个权重。权重 w 使用 super_block_scale 和 importance matrix 获得，结果为每权重 2.06 位。
IQ2_SHF2 位量化（q）。超级块有 256 个权重。权重 w 使用 super_block_scale 和 importance matrix 获得，结果为每权重 2.5 位。
IQ2_XSHF2 位量化（q）。超级块有 256 个权重。权重 w 使用 super_block_scale 和 importance matrix 获得，结果为每权重 2.31 位。
IQ1_SHF1 位量化（q）。超级块有 256 个权重。权重 w 使用 super_block_scale 和 importance matrix 获得，结果为每权重 1.56 位。
IQ1_MGH1 位量化（q）。超级块有 256 个权重。权重 w 使用 super_block_scale 和 importance matrix 获得，结果为每权重 1.75 位。

如果上表有任何不准确之处，请在此文件上开启 PR。

最后于 更新